某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件 B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
解:(1)设该商店购进一件A种纪念品需要a元,购进一件B种纪念品需要b元
则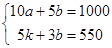
∴解方程组得
∴购进一件A种纪念品需要50元,购进一件B种纪念品需要100元
(2)设该商店购进A种纪念品x个,购进B种纪念品y个
∴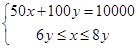
解得20≤y≤25
∵y为正整数 ∴共有6种进货方案
(3)设总利润为W元
W =20x+30y=20(200-2 y)+30y
=-10 y+4000 (20≤y≤25)
∵-10<0∴W随y的增大而减小
∴当y=20时,W有最大值
W最大=-10×20+4000=3800(元)
∴当购进A种纪念品160件,B种纪念品20件时,可获最大利润,最大利润是3800元
(1)关系式为:A种纪念品10件需要钱数+B种纪念品5件钱数=1000;A种纪念品5件需要钱数+B种纪念品3件需要钱数=550;
(2)关系式为:购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,拿出1万元全部用来购进这两种纪念品,得出不等式组求出即可;
(3)设总利润为W元,例出W与y的关系式,进行解答
