问题
解答题
我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种苗木,由信息解答以下问题:
小题1:设装A种苗木车辆数为x,装运B种苗木的车辆数为y,求y与x之间的函数关系式; 小题2:若装运每种苗木的车辆都不少于2辆,则车辆安排方案有几种?写出每种安排方案 小题3:若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润。 |
答案
小题1:由装A种为x辆,装B种为y辆,装C种为(10-x-y)辆,
由题意得:12x+10y+8(10-x-y)=100
∴y=10-2x…… (2分)
小题2:∵10-x-y=10-x-(10-2x)=x,
故装C种车也为 x 辆.
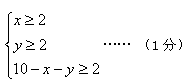
解得:2≤x≤4,
.∵x应取整数,∴x=2或x=3或x=4,
∴车辆的安排方案有三种.
方案一:安排2辆汽车运A品种,6辆汽车运B品种,2辆汽车运C品种;…… (1分)
方案二:安排3辆汽车运A品种,4辆汽车运B品种,3辆汽车运C品种;…… (1分)
方案三:安排4辆汽车运A品种,2辆汽车运B品种,4辆汽车运C品种.…… (1分)
小题3:设销售利润为W(万元),则W=3×12x+4×10×(10-2x)+2×8x=-28x+400,…(2分)∵k=-28<0,∴W随x的减小而增大,
∴当x=2时,W取最大值,W最大值=344.…… (2分)
即应采用方案一可获得最大利润,最大利润为344万元.
(1)根据题意列式:12x+10y+8(10-x-y)=100,变形后即可得到y=-2x+10;
(2)根据装运每种水果的车辆数都不少于2辆,x≥2,y≥2,解不等式组即可;
(3)结合题意,设最大利润为W(万元),依题意可列出表示式,W=-28x+400,可知函数为减函数,即可得出当x=2时,W最大.
