（1）双曲线C的右准线l的方程为：x=

a2

c

，两条渐近线方程为：y=±

b

a

x．

∴两交点坐标为　P(

a2

c

，

ab

c

)、Q(

a2

c

，-

ab

c

)．

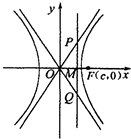
设M为PQ与x轴的交点

∵△PFQ为等边三角形，则有|MF|=

3

2

|PQ|（如图）．

∴c-

a2

c

=

3

2

•(

ab

c

+

ab

c

)，即

c2-a2

c

=

3 ab

c

．

解得　b=

3

a，c=2a．

∴e=

c

a

=2．

（2）由（1）得双曲线C的方程为

x2

a2

-

y2

3a2

=1．直线方程为y=ax+

3

a

把y=ax+

3

a代入得(a2-3)x2+2

3

a2x+6a2=0．

依题意　

a2-3≠0 △=12a4-24(a2-3)a2＞0

∴a²＜6，且a²≠3．

设P（x₁，y₁），Q（x₂，y₂），

∴x1+x2=

2 3 a2

3-a2

，x1x2=

6a2

a2-3

∴双曲线C被直线y=ax+b截得的弦长为l=

(x1-x2)2+(y1-y2)2

=

(1+a2)(x1-x2)2

=

(1+a2)[(x1+x2)2-4x1x2]

=

(1+a2) 12a4-24(a2-1)a2 (a2-3)2

∵l=

b2e2

a

=12a．

∴144a2=(1+a2)•

72a2-12a4

(a2-3)2

．

整理得　13a⁴-77a²+102=0．

∴a²=2或a2=

51

13

．

∴双曲线C的方程为：

x2

2

-

y2

6

=1或

13x2

51

-

13y2

153

=1．