问题
解答题
双曲线
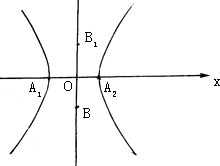
(1)求双曲线的方程; (2)若B1是双曲线虚轴在y轴正半轴上的端点,过点B作直线交双曲线于点M,N,求
|
答案
(1)∵A(a,0),B(0,-b),∴设直线AB:
-x a
=1y b
∴
,∴
=b a 3
=ab a2+b2 3 2
,a= 3 b=3
∴双曲线方程为:
-x2 3
=1.y2 9
(2)∵双曲线方程为:
-x2 3
=1,y2 9
∴A1(-
,0),A2(3
,0),设P(x0,y0),3
∴kPA1=
,kPA2=y0 x0+ 3
,y0 x0- 3
∴k1k2=
=y02 x02-3
=3.3x02-9 x02-3
B(0,-3)B1(0,3),设M(x1,y1),N(x2,y2)
∴设直线l:y=kx-3,
∴
,y=kx-3 3x2-y2=9
∴3x2-(kx-3)2=9.
(3-k2)x2+6kx-18=0,
∴x1+x2=
y1+y2=k(x1+x2)-6=6k k2-3
x1x2=18 k2-3
y1y2=k2(x1x2)-3k(x1+x2)+918 k2-3
∵
=(x1,y1-3)B1M
=(x2,y2-3)B1N
∵
•B1M
=0B1N ∴x1x2+y1y2-3(y1+y2)+9=0
+9-18 k2-3
+9=054 k2-3
k2=5,即k=±
代入(1)有解,5
∴lMN:y=±
x-3.5
