问题
解答题
已知数列{an}中a1=
(1)求证数列{bn]是等差数列; (2)若Sn=(a1-1)•(a2-1)+(a2-1)•(a3-1)+…+(an-1)•(an+1-1),则Sn是否存在最大值或最小值?若有,求出最大值与最小值,若没有说明理由. |
答案
(1)由题意知bn=
,∴bn-bn-1=1 an-1
-an-1 an-1-1
=1(n∈N*),1 an-1-1
∴数列{bn]是首项为b1=
=-1 a1-1
,公差为1的等差数列.5 2
(2)依题意有.an-1=1 n- 7 2
Sn=(a1-1)•(a2-1)+(a2-1)•(a3-1)+…+(an-1)•(an+1-1)=-
-2 5
,1 n- 5 2
设函数y=
,则函数在(1 x- 5 2
,+∞)上为减函数.5 2
Sn在[3+∞)上是递增,且Sn<-
,故当n=3时,且Sn=-2 5
-2 5
,取最小值-1 n- 5 2
.12 5
而函数y=
在(-∞,1 x- 5 2
)上也为减函数,Sn在(1,2]上是递增,且Sn>-5 2
,2 5
故当n=2时,Sn取最大值:S2=
.Sn的最大值为8 5
.8 5

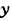 +
+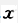 )e
)e