RSA是一种公开密钥加密算法。假定
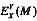 表示利用X的密钥Y对消息M进行加密,
表示利用X的密钥Y对消息M进行加密,
 表示利用X的密钥Y对消息M进行解密,其中Y=P表示公钥,Y=S表示私钥。A利用RSA进行数字签名的过程可以表示为______,A利用RSA实施数字签名后不能抵赖的原因是______。
表示利用X的密钥Y对消息M进行解密,其中Y=P表示公钥,Y=S表示私钥。A利用RSA进行数字签名的过程可以表示为______,A利用RSA实施数字签名后不能抵赖的原因是______。
A.算法是有效的
B.是A而不是第三方实施的签名
C.只有A知道自己的私钥
D.A公布了自己的公钥,且不可伪造
参考答案:C
解析: RSA是一种具有代表性的公钥加密算法,其理论基础是寻找大素数是相对容易的,而分解两个大素数的积在计算上是不可行的。依题意,公钥KU={e,n),私钥KR={d,n},收发双方均已知n,发方已知e,只有收方已知d。若使用RSA算法将明文M加密为密文C,则加密的过程可表示为C=Memod n;解密的过程可表示为M=Cdmod n=(Me)dmod n=Medmod n。
数字签名是笔迹签名的模拟,用于保证信息传输的完整性、发送者的身份认证,以及防止交易中的抵赖行为等。依题意,发方A利用RSA进行数字签名的过程是,A使用消息摘要算法(如MD5)计算出明文的摘要M,接着用A的私钥对消息M进行加密,得到密文
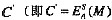 ,以此代表A对消息M的签名信息),再用A从CA机构中获得的B的公钥对密文C’进行加密,得到密文C’’(即
,以此代表A对消息M的签名信息),再用A从CA机构中获得的B的公钥对密文C’进行加密,得到密文C’’(即
 ,然后将消息M和密文C’’通过网络传送给B;收方B收到密文C’’后先使用自己的私钥对其进行解密,得到密文
,然后将消息M和密文C’’通过网络传送给B;收方B收到密文C’’后先使用自己的私钥对其进行解密,得到密文
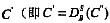 ,再用B从CA机构中获得的A的公钥对密文C’进行解密,得到消息
,再用B从CA机构中获得的A的公钥对密文C’进行解密,得到消息
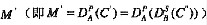 ;如果解密出的M’与消息M相同,则认为签名是有效的,反之则认为签名是无效的。在交易过程中,如果发方A想抵赖自己曾经发送过C’’时,第三方仲裁机构则可以根据“只有发方A知道自己的私钥,因此只有发方能够产生有效的签名”的理由,驳回A的抵赖行为。
;如果解密出的M’与消息M相同,则认为签名是有效的,反之则认为签名是无效的。在交易过程中,如果发方A想抵赖自己曾经发送过C’’时,第三方仲裁机构则可以根据“只有发方A知道自己的私钥,因此只有发方能够产生有效的签名”的理由,驳回A的抵赖行为。
