问题
解答题
煤炭是攀枝花的主要矿产资源之一,煤炭生产企业需要对煤炭运送到用煤单位所产生的费用进行核算并纳入企业生产计划.某煤矿现有1000吨煤炭要全部运往A.B两厂,通过了解获得A.B两厂的有关信息如下表(表中运费栏“元/t•km”表示:每吨煤炭运送一千米所需的费用):
|
答案
解:(1)若运往A厂x吨,则运往B厂为(1000﹣x)吨.
依题意得:y=200×0.45x+150×a×(1000﹣x)
=90x﹣150ax+150000a,
=(90﹣150a)x+150000a.
依题意得: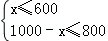
解得:200≤x≤600.
∴函数关系式为y=(90﹣150a)x+150000a,(200≤x≤600).
(2)当0<a<0.6时,90﹣150a>0,
∴当x=200时,y最小=(90﹣150a)×200+150000a=120000a+18000.
此时,1000﹣x=1000﹣200=800.
当a>0.6时,90﹣150a<0,又因为运往A厂总吨数不超过600吨,
∴当x=600时,y最小=(90﹣150a)×600+150000a=60000a+54000.
此时,1000﹣x=1000﹣600=400.
答:当0<a<0.6时,运往A厂200吨,B厂800吨时,总运费最低,最低运费120000a+18000元.
当a>0.6时,运往A厂600吨,B厂400吨时,总运费最低,最低运费60000a+54000.
(1)根据总费用=运往A厂的费用+运往B厂的费用.经化简后可得出y与x的函数关系式,
(2)根据图表中给出的判定吨数的条件,算出自变量的取值范围,然后根据函数的性质来算出所求的方案.
