问题
问答题
求证:不等式
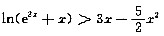 当x>0时成立.
当x>0时成立.
答案
参考答案:[分析与证明] [*]
注意g(0)=0,且
g’(x)=4e2x+5(e2x+x)+(5x-3)(2e2x+1)
=10x(e2x+1)+3(e2x-1)>0(x>0)
[*]0单调增加,由此可得对x>0,有g(x)>g(0)=0从而f’(x)>0,当x>0时成立,于是可得f(x)当x≥0时单调增加,[*]当x>0时成立,移项得原不等式成立.
