设f(x)在[a,b]上可导,在(a,b)内二阶可导,
f(a)=f(b)=0,f’(a)f’(b)>0.
试证:
(Ⅰ)存在ξ∈(a,b),使f(ξ)=0;
(Ⅱ)存在η∈(a,b),使f"(η)=f(η)。
参考答案:
利用极限的保号性及介值定理易证(Ⅰ).对(Ⅱ)可先作辅助函数
ψ(x)=exf(x).
令其导数等于0,可产生
ex[f’(x)+f(x)]=0, 即 f’(x)+f(x)=0.
再作辅助函数F(x)=e-x[f(x)+f’(x)]证之.
证 (Ⅰ)由f’(a)f’(b)>0知,f’(a)与f’(b)同号,不妨设
f’(a)>0,f’(b)>0,
则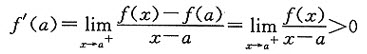
又由极限的保号性知,存在x1∈(a,a+δ1),使得f(x1)>0;同理存在x2∈(b-δ2,b),使得f(x2)<0.
由连续函数的介值定理(零点定理)知,存在ξ∈(x1,x2) (a,b),使得f(ξ)=0.
(a,b),使得f(ξ)=0.
(Ⅱ)令ψ(x)=exf(x),则
ψ(a)=ψ(ξ)=ψ(b).
由罗尔定理知,存在ξ1∈(a,ξ),使
ψ’(ξ1)=[exf(x)]’|x=ξ1=0, 即 f(ξ1)+f’(ξ1)=0.
同理,存在ξ2∈(ξ,b),使
ψ’(ξ2)=eξ2[f(ξ2)+f(ξ2)]=0,
即
f(ξ2)+f’(ξ2)=0.
再令
F(x)=e-x(f(x)+f’(x)),
则
F(ξ1)=F(ξ2)=0.
对F(x)在[ξ1,ξ2]上应用罗尔定理知,存在
使得
F’(η)|x=η={-e-x[f(x)+f’(x)]+e-x[f’(x)+f"(x)]}x=η=e-x[f(x)-f(x)]|x=η=0,
即
F’(η)=e-η[f"(η)-f(η)]=0, 亦即 f"(η)=f(η).
