问题
问答题
设函数f(x)在区间[0,1]上连续,在(0,1)内可导,且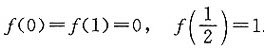
试证:(Ⅰ)存在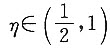 ,使f(η)=η;
,使f(η)=η;
(Ⅱ)对任意实数λ,必存在ξ∈(0,η),使得f’(ξ)-λ[f(ξ)-ξ]=1。
答案
参考答案:
(1)只需作出辅助函数Φ(x)=f(x)-x,利用介值定理证之;
(2)对于中值等式f’(ξ)-λf(ξ)=0,常作辅助函数F(x)=f(x)e-λx证之.将待证等式右边的1看成ξ’,则待证等式可化为
f’(ξ)-ξ’-λ[f(ξ)-ξ]=[f(ξ)-ξ]’-λ[f(ξ)-ξ].
于是易想到作辅助函数
F(x)=e-λx[f(x)-x],
利用罗尔定理证之.
证 (Ⅰ)令Φ(x)=f(x)-x,则Φ(x)在[0,1]上连续,又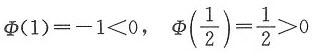
故由介值定理知,存在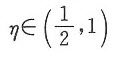 ,使得
,使得
Φ(η)=f(η)-η=0,即f(η)=η.
(Ⅱ)设F(x)=e-λxΦ(x)=e-λx[f(x)-x],
则F(x)在[0,η]上连续,在(0,η)内可导,且
F(0)=0,F(η)=e-ληΦ(η)=0,
即F(x)在[0,η]上满足罗尔定理的条件,故存在ξ∈(0,η),使得F’(ξ)=0,即
e-λξ{f’(ξ)-λ[f(ξ)-ξ]-1}=0,
从而
f’(ξ)-λ[f(ξ)-ξ]=1.
