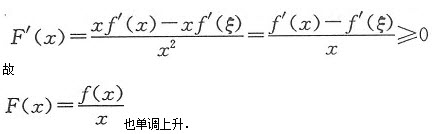问题
问答题
已知f(0)=0，f(x)在[0，+∞)上连续，在(0，+∞)内导数单调上升，证明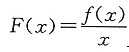
也单调上升。
答案
参考答案：
只需证明F’(x)≥0，注意到f(0)=0，利用此条件可应用拉格朗日中值定理．
证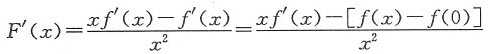
应用拉格朗日中值定理，得到
f(x)-f(0)=xf’(ξ)， 其中ξ∈(0，x)．
因f’(x)单调上升，故f’(x)＞f’(ξ)．于是
搜题请搜索小程序“爱下问搜题”
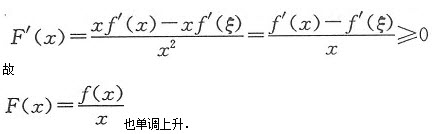
已知f(0)=0，f(x)在[0，+∞)上连续，在(0，+∞)内导数单调上升，证明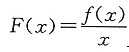也单调上升。
参考答案：
只需证明F’(x)≥0，注意到f(0)=0，利用此条件可应用拉格朗日中值定理．
证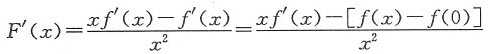
应用拉格朗日中值定理，得到
f(x)-f(0)=xf’(ξ)， 其中ξ∈(0，x)．
因f’(x)单调上升，故f’(x)＞f’(ξ)．于是