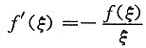问题
问答题
设函数f(x)在闭区间[0，1]上可微，且满足
λ∈(0，1)为常数。
求证：在(0，1)内至少存在一点ξ，使f’(ξ)=-f(ξ)/ξ
答案
参考答案：
利用积分中值定理，存在ξ1∈(0，λ)，使f(1)=ξ1f(ξ1)．
如果令
F(x)=xf(x)，
则
F(1)=f(1)=ξ1f(ξ1)=F(ξ1)，
即F(x)在x=1，x=ξ1两点处函数值相等，故可对F(x)在(ξ1，1)内使用罗尔定理．
证 令F(x)=x(x)，显然F(x)在[0，1]上可微．
应用积分中值定理得
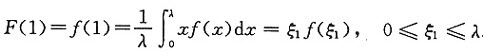
又
F(ξ1)=ξ1f(ξ1)， 则 F(ξ1)=F(1)．
于是对F(x)在[ξ1，1]上应用罗尔定理知，至少存在ξ∈(ξ1，1)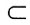
(0，1)，使得
F’(ξ)=ξf’(ξ)+f(ξ)=0， 即