问题
填空题
设A,B是n阶方阵,且AB=BA,其中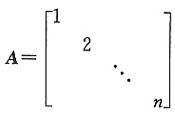
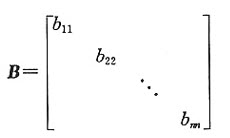
试求矩阵B=()。
答案
参考答案:
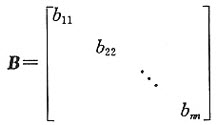
解析:
A为对角矩阵,另一矩阵B与A可交换,则B也必为对角矩阵.下用矩阵乘法推出矩阵B.
设
B=[bij]n×n,AB=[cij]n×n,BA=[dij]n×n,
显然
cij=ibij,dij=jbij.
又因
AB=BA,
故
ibij=jbij(i,j=1,2,…,n),
其中,当i≠j时,有(i-j)bij=0,故bij=0(i≠j).因此