问题
单项选择题
设f（x），g（x）是恒不为零的可导函数，且
f’（x）g（x）-f（x）g’（x）＞0，
则当0＜x＜1时（）。
A．f(x)g(x)＞f(1)g(1)
B．f(x)g(x)＞f(0)g(0)
C．f(x)g(1)＜f(1)g(x)
D．f(x)g(0)＜f(0)g(x)
答案
参考答案：C
解析：
由题设条件
f’(x)g(x)-f(x)g’(x)＞0，
有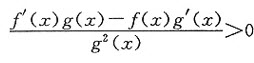
(因g(x)是恒不为零的可导函数)，
即
由题设知
由于g(x)是恒不为零的可导函数，因此g(x)连续，从而g(x)保持恒定的符号，故
g(x)g(1)＞0．
于是由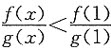
得到
f(x)g(1)＜f(1)g(x)． 仅(C)入选．