某乡A、B两村盛产柑桔,A村有柑桔200吨,B村有柑桔300吨.现将这些柑桔运到C、D两个冷藏室,已知C仓库可储存240吨,D仓库可储存260吨;从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑桔重量为x吨,A、B两村运往两仓库的柑桔运输费用分别为yA元和yB元. (1)请填写下表,并求出yA、yB与x之间的函数关系式:
(3)考虑到B村的经济承受能力,B村的柑桔运费不得超过4830元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值. |
(1)yA=-5x+5000(0≤x≤200),yB=3x+4680(0≤x≤200);
(2)当40<x≤200时,yA<yB即A村费用较小;
(3)当A村调往C仓库的柑桔重量为50吨,调往D仓库为150吨,B村调往C仓库为190吨,调往D仓库110吨的时候,两村的运费之和最小,最小费用为9580元.
题目分析:(1)利用运送的吨数×每吨运输费用=总费用,即可列出函数解析式;
(2)由(1)中的函数解析式联立方程与不等式解答即可;
(3)首先由B村的荔枝运费不得超过4830元得出不等式,再由两个函数和,根据自变量的取值范围,求得最值.
(1)A,B两村运输荔枝情况如表,
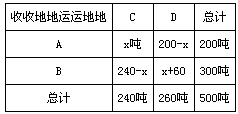
yA=-5x+5000(0≤x≤200),yB=3x+4680(0≤x≤200).
(2)当yA<yB时,-5x+5000<3x+4689,x>40,
当40<x≤200时,yA<yB即A村费用较小.
(3)由yB≤4830,3x+4680≤4830,∴x≤50,
设两村运费之和为y,∴y=yA+yB,即:y=-2x+9680.
又∵0≤x≤50时,y随x增大而减小.
∴当x=50时,y有最小值,y最小值=9580(元).
答:当A村调往C仓库的柑桔重量为50吨,调往D仓库为150吨,B村调往C仓库为190吨,调往D仓库110吨的时候,两村的运费之和最小,最小费用为9580元.
点评:解答本题的关键是熟练掌握基本数量关系:运送的吨数×每吨运输费用=总费用列出函数解析式,进一步由函数解析式分析解决问题.
