水果商李老板在高州市收购有香蕉120吨,在海口市收购有香蕉60吨,现要销往北京100吨,沈阳80吨(全部用汽车运输).已知从高州运一吨香蕉到北京和沈阳分别需800元和1000元;从海口运一吨香蕉到北京和沈阳分别需1000元和1300元.
(1)设从海口运往北京x吨,求总运费y(元)关于x(吨)的函数关系式;
(2)李老板计划用17万元开支运费,够用吗?
(3)若每辆车装10吨,且不能浪费车力.李老板要把总运费控制在不超过17.5万元,有多少种调运方案可实现?
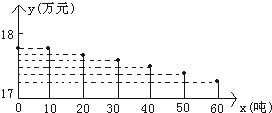
(4)请根据前面的要求画出这一函数的图象.
(1)y=﹣100x+178000(0≤x≤60)
(2)不够用
(3)如表
| 运往地方 数量 产地 | 北京 | 沈阳 | ||||||
| 高州 | 70 | 60 | 50 | 40 | 50 | 60 | 70 | 80 |
| 海口 | 30 | 40 | 50 | 60 | 30 | 20 | 10 | 0 |
题目分析:(1)以从海口运往北京x吨作为着手点,依次列出从海口运往沈阳、从高州运往北京、从高州运往沈阳的香蕉吨数的表达式.再根据运费=运费单价×吨数,列出总运费y关于x的函数表达式,进行化简.
(2)根据(1)中总运费y(元)关于x(吨)的函数关系式,与自变量x的取值范围,求出总运费的最小值与17万元比较.
(3)根据(1)中总运费y(元)关于x(吨)的函数关系式,与自变量x的取值范围,列出总运费,一元一次不等式,求出x的取值范围,并且每种方案的x均能被10整除.
(4)画出坐标系,标出各对应点.
解:(1)依题意知,从海口运往沈阳的香蕉为(60﹣x)吨,从高州运往北京的香蕉为(100﹣x)吨,从高州运往沈阳的香蕉为[120﹣(100﹣x)]吨,则y=1000x+1300(60﹣x)+800(100﹣x)+1000[120﹣(100﹣x)]
化简整理y=﹣100x+178000(0≤x≤60)
(2)由y=﹣100x+178000(0≤x≤60)可知y的最小值为:
y=﹣100×60+178000=172000(元)
∵170000<172000
∴李老板计划用17万元开支运费不够用;
(3)总运费控制在不超过17.5万元,得﹣100x+178000≤175000,解得x≥30
依题意知x可以取30、40、50、60,即有四种调运方案,具体安排见下表
| 运往地方 数量 产地 | 北京 | 沈阳 | ||||||
| 高州 | 70 | 60 | 50 | 40 | 50 | 60 | 70 | 80 |
| 海口 | 30 | 40 | 50 | 60 | 30 | 20 | 10 | 0 |
| x(吨) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| y(万元) | 17.8 | 17.7 | 17.6 | 17.5 | 17.4 | 17.3 | 17.2 |

点评:本题考查一次函数的应用.本题内容较多,特别注意以从海口运往北京x吨作为着手点,依次列出从海口运往沈阳、从高州运往北京、从高州运往沈阳的香蕉吨数的表达式.
