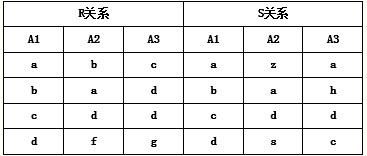
关系R、S如表4-48所示,R÷(πA1,A2(σ1<3(S)))的结果为 (1) ,左外连接、右外连接和完全外连接的元组个数分别为 (2) 。
表4-48 关系R、S
(2)处填()。
A.2,2,4
B.2,2,6
C.4,4,6
D.4,4,4
参考答案:C
解析:
首先看除法运算的定义。设两个关系R和S的元数分别为r和s(设r>s>0),那么R÷S是一个(r-s)元的元组的集合。R÷S是满足下列条件的最大关系:其中每个元组t与S中每个元组u组成的新元组<t,u>必在关系R中。其具体计算公式如下:
R÷S=π1,2,…,r-s(R)-π1,2,…,r-s((π1,2,…,r-s(R)×S)-R)
在本题中πA1,A2(σ1<3(S))的结果如表4-50所示。
表4-50 新的关系S
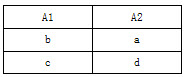
直接把R和新的S结果代入上述公式进行计算肯定不行,必须用基于像集的方法计算,可得R÷S={d}。
两个关系R和S进行自然连接时,选择两个关系R和S公共属性上相等的元组,去掉重复的属性列构成新关系。这样,关系R中的某些元组有可能在关系S中不存在公共属性值上相等的元组,造成关系R中这些元组的值在运算时舍弃了;同样,关系S中的某些元组也可能舍弃。为此,扩充了关系运算左外连接、右外连接和完全外连接。
左外连接:R和S进行自然连接时,只把R中舍弃的元组放到新关系中。
右外连接:R和S进行自然连接时,只把S中舍弃的元组放到新关系中。
完全外连接:R和S进行自然连接时,把R和S中舍弃的元组都放到新关系中。
根据以上定义,本题中R与S的左外连接、右外连接和完全外连接的结果如表4-51~表4-53所示。
[*]
