问题
问答题
求函数y=ln(1+x2)的单调区间、极值、凹凸区间和拐点.
答案
参考答案:
函数定义域为x∈R,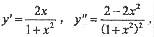
令y’=0得x=0,令y”=0得x=±1.

函数y=ln(1+x2)的单调增加区间为(0,+∞),
单调减少区间为(-∞,0),
y(0)=0为极小值.
函数y=ln(1+x2)的凸区间为(-∞,-1)∪(1,+∞),
凹区间为(-1,1),
拐点为(-1,ln2)与(1,ln2).
求函数y=ln(1+x2)的单调区间、极值、凹凸区间和拐点.
参考答案:
函数定义域为x∈R,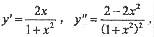
令y’=0得x=0,令y”=0得x=±1.

函数y=ln(1+x2)的单调增加区间为(0,+∞),
单调减少区间为(-∞,0),
y(0)=0为极小值.
函数y=ln(1+x2)的凸区间为(-∞,-1)∪(1,+∞),
凹区间为(-1,1),
拐点为(-1,ln2)与(1,ln2).