假设某完全竞争行业有100个相同的厂商。每个厂商的成本函数为：
TC=0.1Q2+Q+10
求：(1)市场供给函数。
(2)假设市场需求函数为Qd=4 000-400P，求市场的均衡价格和产量。
(3)假定对每单位产品征收0.9元的税，新的市场均衡价格和产量又为多少厂商和消费者的税收负担各为多少
参考答案：
解析：已知代表性厂商的成本函数为：为TC=0.1q2+q+10则
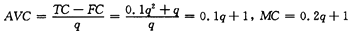
显然，当任何产量下(产量一定大于或等于0)MC=AVC，故厂商的短期供给函数P=MC，即厂商的短期供给函数为P=0.2q+1，也即q=5P=5(p=1)。
该行业有100个相同的厂商，行业的供给曲线是各个厂商的供给曲线水平方向的相加，故行业的短期供给曲线也即供给函数为：Q=(5P-5)×100，即Qs=500P-500(P=1)。
(2)已知市场需求函数为Qd=4 000-400P，而市场供给函数也即行业供给函数已经计算出来Qs=500P-500，市场均衡时Qs=Qd，即500P-500=4 000-400P，因而市场均衡价格P=5元，市场均衡产量Qs=Qd=4 000-400×5=2 000。
(3)征收单位产品税，意味着产品的成本增加，从而供给价格上升，也就是说，在同样的价格水平上，现在供给更少了。因此，原来的行业的总供给函数为Q=500P-500，征税以后变为=500(P-t)-500，其中t为单位产品税。现在已知每单位产品征收0.9元的税，因此行业的供给函数为=500(P-0.9)-500，行业的需求函数仍为Qd=4 000-400P。市场均衡时，
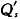=Qd即500(P-0.9)-500=4 000-400P，所以新的市场均衡价格P=5.5元，新的市场均衡产量为：
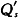=Qd=500(5.5-0.9)-500=1 800。
由于税收的作用，产品的价格提高了0.5元。但整个行业的销售量下降了200单位(1 800-2 00.0=-200)。进一步分析发现，价格提高的数量(5.5元-5元=0.5元)小于每单位产品的税收的数量0.9元。可见，在0.9元的税收中，有0.5元通过价格转移到消费者身上，剩余的0.4元由厂商来承担。