问题
问答题
(Ⅰ)设D=(x,y)|a≤x≤b,c≤y≤d|,若f"xy与f"yx在D上连续,证明
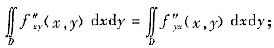
(Ⅱ) 设D为Oxy平面上的区域,若f"xy与f"yx都在D上连续,证f"xy与f"yx在D上相等.
答案
参考答案:本题考查二重积分的计算,但是比较新颖的非常规考题,涉及抽象的理论推导,在2011年考研中已经有所涉及,本题的设计同样比较独特,希望考生多加体会和总结。
(Ⅰ)证明[*]
同理,[*]
结论成立.
(Ⅱ)证明 用反证法.设[*]P0(x0,y0)∈D,有f"xy(x0,y0)≠f"xy(x0,y0).不妨设f"xy(x0,y0)-f"yx(x0,y0)>0,由于
[*]
由极限的保号性,[*]ε0>0,[*]δ>0,当P(x,y)∈U(P0,δ)时有f"xy(x,y)-f"yx(x,y)>ε0,取
[*]
于是,
[*]
由(Ⅰ),[*],出现矛盾.故f"xy(x,y)与f"yx(x,y)在D上都相等.