问题
问答题
求微分方程xy’=3y-6x2的一个解y=y(x),使得曲线y=y(x)与直线x=1,y=0所围成的平面图形绕x轴旋转一周所得旋转体体积最小。
答案
参考答案:方程xy’=3y-6x2化为
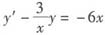 ,其通解为
,其通解为
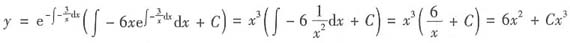
旋转体体积
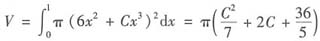 ,
,
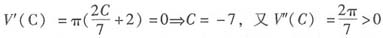 ,在C=-7处取极小值
,在C=-7处取极小值
故C=-7时,体积V最小,所以y=6x2-7x3。
解析:[考点] 微分方程的解及微积分在几何中的应用
求微分方程xy’=3y-6x2的一个解y=y(x),使得曲线y=y(x)与直线x=1,y=0所围成的平面图形绕x轴旋转一周所得旋转体体积最小。
参考答案:方程xy’=3y-6x2化为
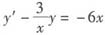 ,其通解为
,其通解为
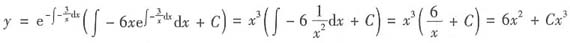
旋转体体积
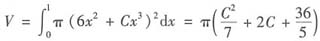 ,
,
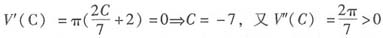 ,在C=-7处取极小值
,在C=-7处取极小值
故C=-7时,体积V最小,所以y=6x2-7x3。
解析:[考点] 微分方程的解及微积分在几何中的应用