问题
问答题
设f(x)单调且具有一阶连续导数，z=f(x+φ(y))满足
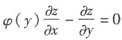，求可导函数φ(y)。
答案
参考答案：
，
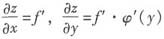代入方程
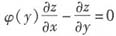，得φ(y)·f’-f’φ’(y)=0，
即φ’(y)=φ(y)，解得φ(y)=Cex，其中C为任意常数。
解析：[考点] 二元函数的导数
搜题请搜索小程序“爱下问搜题”
设f(x)单调且具有一阶连续导数，z=f(x+φ(y))满足
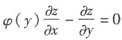，求可导函数φ(y)。
参考答案：
，
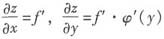代入方程
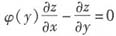，得φ(y)·f’-f’φ’(y)=0，
即φ’(y)=φ(y)，解得φ(y)=Cex，其中C为任意常数。
解析：[考点] 二元函数的导数