问题
问答题
设二次型
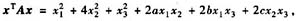
矩阵A满足AB=0，其中
求(A-3E)6。
答案
参考答案：因为A～A，有A-3E～A-3E，进而(A-3E)6～(A-3E)6，又A-3E=[*]，所以由Q-1AQ=A得Q-1(A-3E)6Q=(A-3E)6=36E。于是
(A-3E)6=Q(A-3E)6Q-1=Q(36E)Q-1=36E
解析：[*]
搜题请搜索小程序“爱下问搜题”
设二次型
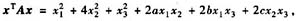
矩阵A满足AB=0，其中
求(A-3E)6。
参考答案：因为A～A，有A-3E～A-3E，进而(A-3E)6～(A-3E)6，又A-3E=[*]，所以由Q-1AQ=A得Q-1(A-3E)6Q=(A-3E)6=36E。于是
(A-3E)6=Q(A-3E)6Q-1=Q(36E)Q-1=36E
解析：[*]