问题
解答题
某商店进了一批服装,进货单价为50元,如果按每件60元出售,可销售800件,如果每提价1元,其销售量减少20件,
(1)现要获利12000元,且销售成本不超过24000元,问这种服装销售单价应确定为多少元适宜?这时应进多少服装?
(2)12000是不是可能获得的最大利润?如果是,说明理由;如果不是,请求出最大利润是多少?
答案
(1)设在60元基础上再提高x元,则有
(10+x)(800-20x)=12000,
整理化简得:x2-30x+200=0,
解得x1=10,x2=20,
当x=10时,定价为70元,销售成本为50×(800-200)=30000元>24000元,不符合题意,
当x=20时,定价为80元,销售成本为50×(800-400)=20000元<24000元,符合题意,
故定为80元适宜,此时应进服装400件.
(2)设利润为y=(10+x)(800-20x)=-20(x-15)2+12500,
当x=15,定价为60+x=75元时,可获得最大利润:12500元,
而此时销售成本为25000元大于24000元,要使销售成本不大于24000元,则x≥16.
当x=16时,y=12480元>12000元.
故12000元不是最大利润,当定价为76元时,可获得最大利润12480元.

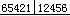 缺失属于Kennedy分类第()
缺失属于Kennedy分类第()