问题
填空题
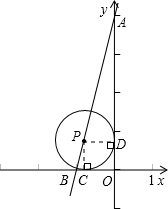
在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(-1,0),以线段AB上一点P为圆心作圆与OA,OB均相切,则点P的坐标为______.
答案
过P作PD⊥y轴于D,PC⊥x轴于C,
设⊙P的半径是x,
∵PD⊥y轴,PC⊥x轴,
∴∠PCO=∠PDO=90°,
又∵∠COD=90°,
∴四边形PCOD是矩形,
又∵PC=PD,
∴四边形PCOD是正方形,
∵PC∥y轴,
∴△PBC∽△ABO,
∴BC:OB=PC:OA,
∴(1-x):1=x:4,
解得x=
,4 5
故P点坐标是(-
,4 5
).4 5
故答案是(-
,4 5
).4 5