问题
问答题
已知函数f(x，y)具有二阶连续偏导数，且f(1，y)=0，f(x，1)=0，
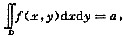其中D=(x，y)|0≤x≤1，0≤y≤1，计算二重积分
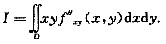
答案
参考答案：[解法一] 因为f(1，y)=0，f(x，1)=0，所以f’y(1，y)=0，f’x(x，1)=0从而
[*]
[*]
[解法二] [*]
在这个过程中也用到了f(1，y)=0，f(x，1)=0，f’y(1，y)=0，f’x(x，1)=0．
解析：
[分析]： 已知积分[*]是关于f(x，y)的积分，而要计算的积分[*]是关于f"xy(x，y)的积分，因此，应将二重积分化为累次积分，然后通过分部积分将二者联系起来．