参考答案：

(1)由题意f(x)=x²|x-2|。

当x＜2时，f(x)=x²(2-x)=x，解得x=0，或x=1；

当x≥2时，f(x)=x²(x-2)=x，解得，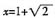

综上所述，所求解集为。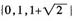

(2)设此最小值为m。

①当a≤1时，在区间[1，2]上f(x)=x³-ax²。

因为，

则f(x)是区间[1，2]上的增函数，所以m=f(1)=1-a。

②当1＜a≤2时，在区间[1，2]上f(x)=x²|x-a|≥0，由f(a)=0知m=f(a)=0。

③当a＞2时，在区间[1，2]上，f(x)=a²-x³。

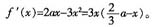
若a≥3，在区间(1，2)内，f’(x)＞0，从而f(x)为区间[1，2]上的增函数，

由此得：m=f(1)=a-1。