问题
问答题
已知向量a=（cosα，sinα），b=（cosβ，sinβ），c=（-1，0）。
（1）求向量b+c的长度的最大值；
（2）设
，且α⊥（b+c），求cosβ的值。
答案
参考答案：
(1)因|b|=1，|c|=1，|b+c|≤|b|+|c|=2，当cosβ=-1时，有|b+c|=(-2，0)，即|b+c|=2，b+c的长度的最大值为2。
(2)若
，则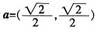
，又由b=(cosβ，sinβ)，c=(-1，0)得，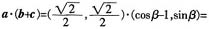
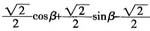，又因为a⊥(b+c)，故a·(b+c)=0，即sinβ=1-cosβ，两边平方得sin2β=(1-cosβ)2，化简得cosβ(cosβ-1)=0，解得cosβ=0或cosβ=1，经检验，cosβ=0或cosβ=1即为所求。