问题
问答题
已知数列an的前n项和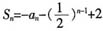
（n为正整数）。令bn=2nan，求证数列（bn）是等差数列，并求数列an的通项公式。
答案
参考答案：
在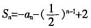
中，令n=1，可得S1=-a1-1+2=a1，即
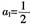。当n≥2时，
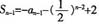，则an=
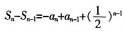，故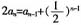
，即2nan=2n-1an-1+1。因bn=2nan，故bn=bn-1+1，即当n≥2时，bn-bn-1=1。又b1=2a1=1，故数列{bn}是首项和公差均为1的等差数列。于是bn=1+(n-1)·1=n=2nan，因此
。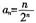