问题
问答题
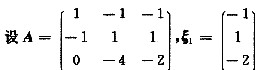
(Ⅰ)求满足Aξ2=ξ1,A2ξ3=ξ1的所有向量ξ2,ξ3;
(Ⅱ)对(I)中的任意向量ξ2,ξ3,证明ξ1,ξ2,ξ3线性无关.
答案
参考答案:(Ⅰ)对于方程组Ax=ξ1,由增广矩阵[*]作初等行变换,有
[*]
令x2=t得x3=1-2t,x1=-t.
所以 ξ2=(-t,t,1-2t)T,t为任意常数.
[*]
(Ⅱ)由(Ⅰ)知
[*]
所以ξ1,ξ2,ξ3线性无关.
[评注] (Ⅰ)中,对于方程组Ax=ξ1,若选x3=t为自由变量,则
[*]
(Ⅱ)中关于ξ1,ξ2,ξ3线性无关的证明也可用定义法.
由题设可知Aξ1=0.如果
k1ξ1+k2ξ2+k3ξ3=0 ①
用A左乘①式两端,并把Aξ1=0代入,有
k2Aξ2+k3Aξ3=0
即 k2ξ1+k3Aξ3=0 ②
用A左乘②式两端,有
k3A2ξ3=0
即 k3ξ1=0.
由于ξ1≠0,故k3=0.代入②可得k2=0.把k2=0,k3=0代入①式,可得k1=0.从而ξ1,ξ2,ξ3线性无关.
