问题
问答题
已知二次型
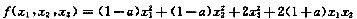的秩为2．
(Ⅰ)求a的值；
(Ⅱ)求正交变换x=Qy把f(x1，x2，x3)化为标准形；
(Ⅲ)求方程f(x1，x2，x3)=0的解．
答案
参考答案：(Ⅰ)由于二次型f的秩为2，即二次型矩阵
[*]
得到矩阵A的特征值是λ1=λ2=2，λ3=0．
对于λ=2，由(2E-A)x=0
[*]
得特征向量α1=(1，1，0)T，α2=(0，0，1)T
对λ=0由(0E-A)x=0
[*]
得特征向量α3=(1，-1，0)T
由于α1，α2，α3已两两正交，单位化有
[*]