问题
问答题
设随机变量X与Y独立,X服从正态分布N(μ,σ2),Y服从[-π,π]上的均匀分布,试求Z=X+Y的概率分布密度(计算结果用标准正态分布函数Φ(x)表示,其中
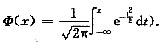
答案
参考答案:[分析与解答] 已知X与Y独立,
X的概率密度为[*]
Y的概率密度[*]由此可求得(X,Y)的概率密度f(x,y)=fX(x)fY(y).我们要求Z=g(x,y)=X+Y的概率密度fZ(z),通常有两种方法.
解法一(分布函数法)先求Z=X+Y的分布函数
[*]
由此得Z的概率密度
[*]
解法二(公式法)由于X与Y独立,Z=X+Y,所以由卷积公式得Z的概率密度
[*]
[*]

 ()
()