问题
问答题
[说明]
某大学城图书馆需要在无线阅览厅的某些位置上放置无线接入点AP(Access Poin)。假设每个无线 AP覆盖范围的半径是6米,因此必须使得每台笔记本电脑上的无线网卡到某个无线AP的直线距离不超过6米。为了简化问题,假设所有无线网卡在同一直线上,并且无线AP沿该直线放置。该问题可以建模为如图1-13所示,其中直线表示无线网卡所在的直线,实心正方形表示无线网卡。现采用贪心策略实现用尽可能少的无线AP覆盖所有的无线网卡。
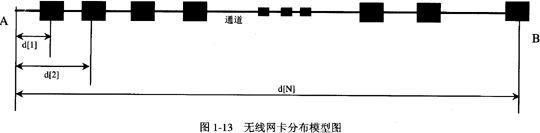
实现贪心算法的流程如图1-14所示。其中,①d[i](1≤i≤N)表示第i张无线网卡到通道A端的距离,N表示无线网卡的总数,无线网卡的编号按照无线网卡到通道A端的距离从小到大进行编号:②s[k]表示第k(k≥1)个无线AP到通道A端的距离。算法结束后k的值为无线AP的总数。
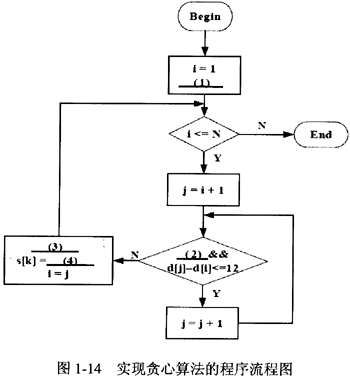
[问题2]
该贪心算法的时间复杂度为 (5) 。
答案
参考答案:[问题2]
虽然该贪心算法中包含两个循环,但实际上只是遍历所有无线网卡一次,因此算法复杂度是O(N)。
