（1）y=5x+10500；（2）12335元；（3）A种酒0瓶，B种酒700瓶．

题目分析：（1）根据等量关系：获利y元=A种品牌的酒的获利+B种品牌的酒的获利，即可得到关系式；

（2）关系式为：A种品牌的酒的成本+B种品牌的酒的成本≥30 000，算出x的最小整数值代入（1）即可

（3）关键描述语是：利润率最大，应选取利润率最大的生产最大数量．

（1）根据题意，得y=20x+15（700-x），即y=5x+10500；

（2）根据题意，得50x+35（700-x）≥30000，解得x≥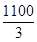=366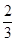

因为x是整数，所以取x=367，代入y=5x+10500，得y=12335

因此每天至少获利12335元；

（3）生产A种酒的利润率为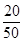=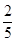；生产B种酒的利润率为=，

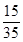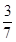因为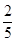<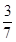，所以要使每天的利润率最大，应生产A种酒0瓶，B种酒700瓶．

点评：解决本题的关键是读懂题意，根据关键描述语找到符合题意的等量关系和不等关系式组．