问题
问答题
某商品需求量Q对p的弹性
(0＜p＜b)，又知该商品的最大需求量为a(a＞0)，求需求量Q对价格p的函数系数．
答案
参考答案：设所求函数关系为Q=Q(p)，根据需求量对价格的弹性
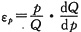
得
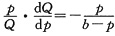，即
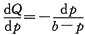
两边积分得通解
lnQ=ln(b-p)+lnC，
即Q=C(b-p)．
又由于最大需求量是指：当价格p→0+时，需求量Q的极限值．依题意有
，
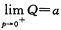即
．
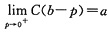确定C=
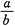，于是Q对p的函数关系为
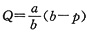
解析： 利用需求价格弹性公式可建立可分离变量的微分方程，再利用初始条件
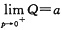(此谓商品的最大需求量)即可求得需求函数Q(p)．