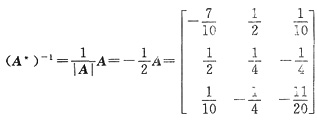问题
问答题
设A为三阶实对称矩阵,且存在可逆矩阵
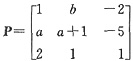 ,
,
使得
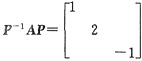
又A的伴随矩阵A*有特征值λ0,λ0所对应的特征向量为α=[2,5,-1]T.
计算(A*)-1
答案
参考答案:由Aα1=1·α1,Aα2=2·α2,Aα3=-1·α3及
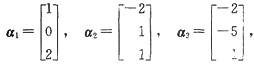
有A[α1,α2,α3]=[α1,2α2,-α3].于是
A=[α1,2α2,-α3][α1,α2,α3]-1
=
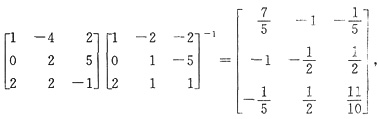
故有
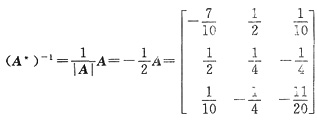
设A为三阶实对称矩阵,且存在可逆矩阵
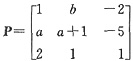 ,
,
使得
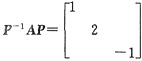
又A的伴随矩阵A*有特征值λ0,λ0所对应的特征向量为α=[2,5,-1]T.
计算(A*)-1
参考答案:由Aα1=1·α1,Aα2=2·α2,Aα3=-1·α3及
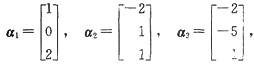
有A[α1,α2,α3]=[α1,2α2,-α3].于是
A=[α1,2α2,-α3][α1,α2,α3]-1
=
故有