问题
问答题
设A为三阶矩阵,α1,α2,α3为三维线性无关列向量组,且有Aα1=α2+α3,Aα2=α3+α1,Aα3=α1+α2.
A是否可对角化
答案
参考答案:由α1,α2,α3线性无关可证明α2-α1,α3-α1,α1+α2+α3线性无关.
事实上,由矩阵表示法:
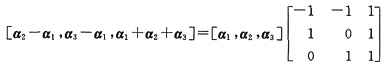 ,
,
而α1,α2,α3线性无关,右边的三阶行列式不等于0,其矩阵可逆,故
α2-α1,α3-α1,α1+α2+α3线性无关,即矩阵A有三个线性无关的特征向量,故矩阵A为可对角化.
解析: 利用所给的向量等式及特征值、特征向量约定义可求出A的全部特征值及三个线性无关的特征向量.
