问题
问答题
设f(x)，g(x)在[a，b]上连续，在(a，b)内可导，证明：存在ξ∈(a，b)，使得
．
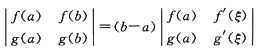答案
参考答案：[证明] 令
，
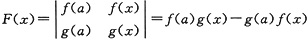则F(x)满足拉格朗日中值定理的各个条件．
因F(a)=f(a)g(a)-g(a)f(a)=0，
F(b)=f(a)g(b)-g(a)f(b)，
则存在ξ∈(a，b)，使
F(b)F(a)=(b-a)F’(ξ)，
即f(a)g(b)-g(a)f(b)=(b-a)[f(a)g’(ξ)-g(a)f’(ξ)]，
亦即
．
解析： 从待证等式出现b-a因子，使人猜想到可能使用拉格朗日中值定理证之．但使用该定理的函数是什么如何找可将待证等式右边中的ξ变为x，去掉导数符号得到
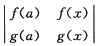=f(a)g(x)-g(a)f(x)，
此为所要找的辅助函数．