参考答案：特征方程为λ+3=0，其特征根为λ=-3，故对应齐次方程的通解为

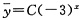，C为任意常数．
因为b=2不是特征根，所以可设非齐次方程的特解形式为

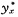=(A₀+A₁x)2^x，
代入非齐次方程得
[A₀+A₁(x+1)]2^x+1+3(A₀+A₁x)2^x=x·2^x，
即[A₀+A₁(x+1)]·2+3(A₀+A₁x)=x．
比较两端同次幂系数，解之得

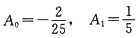
于是所求特解为

．
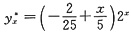因此原方程的通解为

．

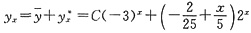解析： f(x)的形式为P_n(x)·b^x，P_n(x)为x的n次多项式，而n=1，b=2．因特征根λ=-3≠2，即f(x)的底数b=2不是特征根，故可设非齐次方程的特解形式为
η^*=(A₀+A₁x)·2^x．将其代入非齐次方程后，比较两端同次幂的系数定出常数A₀，A₁即可求得一特解．