问题
单项选择题
设函数f(x)在x=2的某邻域内可导，且f’(2)=0，又
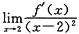=-2，则f(2)______．
A．必是f(x)的极大值
B．必是f(x)的极小值
C．不一定是f(x)的极值
D．一定不是f(x)的极值
答案
参考答案：D
解析： 利用极限的保号性及极值的定义判别之．
仅D入选．由f(x)可导和f’(2)=0知，x=2是f(x)的驻点，但由
，
根据极限保号性及(x-2)2＞0知，当x≠=2时，f’(x)＜0，所以f(2)一定不是f(x)的极值．