问题
单项选择题
设三元二次型f(x1，x2，x3)=XTAX的正惯性指数p=1，且二次型A满足A2+2A-3E=0，则在正交变换下该二次型的标准形是______．
A．
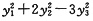
B．
C．
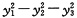
D．
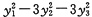
答案
参考答案：D
解析： 先求出A的特征值，确定正负惯性指数，再确定选项．
即Aα=λα，α≠0．
那么由(A2+2A-3E)α=0
有(λ2+2λ-3)α=0，λ2+2λ-3=(λ+3)(λ-1)=0．
由此可知，矩阵A的特征值只能是1或-3．
因为A可逆，正惯性指数p=1，则负惯性指数必为2，所以A的特征值为
λ1=1，λ2=λ3=-3，
从而正交变换下该二次型的标准形为
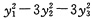．仅D入选．