问题
问答题
设函数f(x)在x=1的某邻域内连续,且有
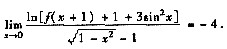
(Ⅰ)求f(1)及

(Ⅱ)求f’(1),若又设f"(1)存在,求f"(1);
(Ⅲ)x=1是否是f(x)的极值点若是,是极大值点还是极小值点
答案
参考答案:[分析与求解] (Ⅰ)由条件知[*]
[*]
又在x=0的某空心邻域内f(x+1)+3sin2x≠0,现利用等价无穷小因子替换:当x→0时,
ln[1+f(x+1)+3sin2x]~f(x+1)+3sin2x,
[*]
[*]
(Ⅱ)方法1° [*]
由[*]在x=1的某邻域内可导
[*]
[*]f"(1)=-2.
方法2° 用泰勒公式.先由一阶泰勒公式得
[*]
[*]f’(1)=0.
当f"(1)存在时,可用二阶泰勒公式得
[*]
[*]f"(1)=-2.
(Ⅲ) 由[*]及极限的不等式性质知,[*]当0<|x|<δ时
[*]即 f(x+1)<0=f(1)
[*]x=1是f(x)的极大值点.
解析:[评注] 题(Ⅲ)是按定义判断函数f(x)在某点取极具值,不能用题(Ⅱ)的结论.因为在题(Ⅲ)中未假设f(x)在点x=0处二阶可导.若又假设f(x)在x=1处二阶可导,则就可用题(Ⅱ)的结论得知,f(x)在点x=1处取极大值.
