阅读下面的文字,完成下面问题。
1986年,中国商业部在新颁发的小麦粉标准里,允许添加过氧化苯甲酰,卫生部同步将过氧化苯甲酰列入《食品添加剂使用卫生标准》。2010年9月中旬,卫生部办公厅在对“关于再次建议尽快出台新的小麦粉国家标准”的答复中表示,遵循技术上确有必要且安全可靠的原则,全国食品添加剂标准委员会已审查并同意注销过氧化苯甲酰(俗称“面粉增白剂”)。
面粉增白剂是中国目前准许使用的1513种(其中包括食品香料1027种)食品添加剂中的一种。所谓食品添加剂是指为改善食品品质和色、香、味,以及为防腐和加工工艺的需要而加入食品中的化学合成物或者天然物质。中国在普通面粉中使用增白剂,已有20多年。多年来,伴随着面粉增白剂的使用产生了种种食品安全问题,并因此而引起了旷日持久的争论。
人们欣赏和喜爱雪白或较白的面粉,这成为增白剂被加入面粉的直接原因。用小麦新加工出来的面粉中含有微量的脂溶性β-胡萝卜素,它呈浅黄色,使得面粉微黄,色泽不佳。但是,这样的面粉经过一段时期的贮存,可以依靠空气中的氧化作用,使脂溶性β-胡萝卜素的共轭双键被自然氧化而破坏,从而改善和提高面粉的色泽。但这需要较长时间。于是,能让面粉立竿见影增白的过氧化苯甲酰被人们选中。添加这种增白剂不仅工艺简单,综合效果也好。增白剂在一定程度上可改善面粉质量,如抑制面粉的霉变,减少面粉长期贮存而产生的霉变风险。因为增白剂放入面粉中会释放原子态氧和苯甲酸,后者是食品工业普遍使用的防腐剂。面粉经过增白剂处理后,可以氧化面粉中的β-胡萝卜素,提高面粉的白度,使得面粉加工设备水平不再成为影响面粉色泽的唯一因素,因而可以使小麦在加工同一等级面粉时相对提高出粉率。这既能提高面粉加工企业的经济效益,也相对增加了粮食产量。同时,采用增白剂后的面粉,可以在几天之内完成熟化过程,让馒头等面食看起来质量更好,体积更大。
专家和研究人员认为,添加少量的增白剂是安全的。然而,现在相当多的人,包括专业人员和公众都认为,面粉中不使用增白剂的利要大于使用增白剂。因为使用增白剂会破坏营养,更会带来很多安全问题,甚至危及人们的健康和生命。
增白剂危害健康的主要表现是它有致癌作用。同时,过氧化苯甲酰是略带刺激性气味的白色粉末,在加热或受到摩擦时易产生爆炸,在一定剂量条件下,对人的皮肤、上呼吸道有确切的刺激性和致敏性。过氧化苯甲酰危害健康还表现在对一些肝脏病人的损害。这种损害恰恰是因为添加了增白剂,即增白剂可以释放出防止面粉霉变的产物苯甲酸。若长期食用含过量添加剂的面粉及其制成品,就会造成苯慢性中毒,给人体健康带来危害,尤其是对肝脏的损害较大。
1997年,欧盟所有的成员国已全部禁用面粉增白剂。在这些国家里,过氧化苯甲酰和三聚氰胺一样,不被允许用于食品生产。可以说,现在我国同意注销过氧化苯甲酰正是为我们的食品安全加了一道保险。(有删改)
1.从原文看,之前有关部门允许在面粉里添加过氧化苯甲酰的根本原因是( )
A.加入过氧化苯甲酰的面粉和面制品可以满足消费者的欣赏需要。
B.面粉中加入过氧化苯甲酰可以满足面粉和面食生产经营者的需要。
C.在规定范围内将过氧化苯甲酰作为食品添加剂是有利并且安全的。
D.将过氧化苯甲酰作为面粉增白剂见效快,工艺简单,综合效果好。
2.下列对文章内容的理解,不正确的一项是( )
A.面粉增白剂在改善和提高面粉色泽的同时,还会在一定程度上抑制面粉的霉变,从而提升面粉的质量。
B.添加了面粉增白剂之后,提高了面粉加工水平,这样就提高了小麦的出粉率,促进了小麦产量的增加。
C.增白剂危害健康的主要表现是它有致癌作用,对人的皮肤、上呼吸道及肝脏可能造成一定的损害。
D.虽然有不同的看法,但现在人们基本达成了使用增白剂会引发包括危及生命在内的食品安全问题的共识。
3.根据原文提供的信息,以下推断正确的一项是( )
A.如果消费者不再将“白”作为面粉、面制品的质量评判标准,那么有关生产经营者就不再需要添加增白剂了。
B.从不同的角度讲,允许或禁止将过氧化苯甲酰等化学合成物作为食品添加剂是各有道理的。
C.食品安全问题数量的多少,事实上是与被允许使用的食品添加剂的数量多少成正比的。
D.从二十多年后过氧化苯甲酰最终被国家同意注销的实例来看,将来弊大于利的食品添加剂不会被人们再使用。
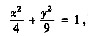 取逆时针方向,则
取逆时针方向,则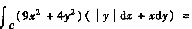 ______.
______.