问题
解答题
已知函数f(x)=
(Ⅰ)求实数m和n的值; (Ⅱ)判断函数f(x)在(-∞,-1]上的单调性,并加以证明. |
答案
(Ⅰ)∵函数f(x)=
是奇函数mx2+2 3x+n
∴f(-x)=-f(x)
∴
=-mx2+2 -3x+n
=mx2+2 3x+n mx2+2 -3x-n
∴n=0
∵f(2)=
.5 3
∴
=4m+2 6 5 3
∴m=2
(II)函数f(x)在(-∞,-1]上是增函数
证明:任取x1 <x2<-1,f(x1) -f(x2) =
(x1+2 3
)-1 x1
(x2+2 3
)=1 x2 2 3
∵x1<x2<-1,∴x1-x2<0,x1x2-1>0(x1-x2) (x1x2-1) x1x2
∴f(x1)-f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)在(-∞,-1]上是增函数

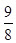 m
m