问题
单项选择题
设
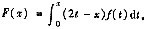其中函数f(x)可导，且f’(x)＞0在区间(-1，1)成立，则
(A) 函数F(x)必在点x=0处取得极大值．
(B) 函数F(x)必在点x=0处取得极小值．
(C) 函数F(x)在点x=0处不取极植，但点(0，F(0))是曲线y=F(x)的拐点．
(D) 函数F(x)在点x=0处不取极值，且点(0，F(0))也不是曲线y=F(x)的拐点．
答案
参考答案：C
解析： 本题主要考查变上限定积分求导法、函数的极值以及曲线的拐点等有关知识．因
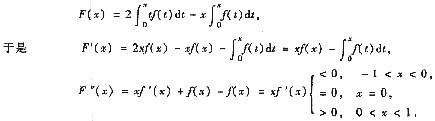
由F’’(x)符号的变化情况知，曲线y=F(x)在区间(-1，0]是凸的，在区间[0，1)是凹的，可见(0，F(0))是其拐点．
由F’’(x)符号的变化情况还知道，F’(0)是F’(x)的最小值，又F’(0)=0，从而知F’(x)＞0当x≠0时成立．这表明F(x)在x=0处不取极值．
综合以上分析知，结论(C)正确，其余均不正确．故应选(C)．