问题
问答题
选择a,b,使(2ax3y3-3y2+5)dx+(3x4y2-2bxy-4)dy是某函数u(x,y)的全微分,并求u(x,y).
答案
参考答案:由于P(x,y)=2ax2y2-3y2+5,Q(x,y)=3x4y2-2bxy-4在整个平面上都有一阶连续偏导数,所以P(x,y)dx+Q(x,y)dy是某一函数全微分的充分必要条件为[*].
即 12x3y2-2by=6ax3y2-6y,所以 a=2,b=3.
于是
[*]
=5x+x4y3-3xy2-4y.

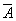 ,则下列结论中正确的是 [ ]
,则下列结论中正确的是 [ ]