问题
填空题
两同心圆的半径分别是10和6,大圆的弦AB长16.AB与小圆的位置关系是______.
答案
过O作OC⊥AB于C,连接OB,
∵OC⊥AB,OC过圆心O,
∴AC=BC=
AB=8,1 2
在Rt△BOC中,由勾股定理得:OC=
=OB2-OC2
=6,102-82
即O到AB的距离等于小圆的半径,
∴AB与小圆的位置关系是相切,
故答案为:相切.
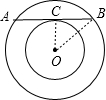
两同心圆的半径分别是10和6,大圆的弦AB长16.AB与小圆的位置关系是______.
过O作OC⊥AB于C,连接OB,
∵OC⊥AB,OC过圆心O,
∴AC=BC=
AB=8,1 2
在Rt△BOC中,由勾股定理得:OC=
=OB2-OC2
=6,102-82
即O到AB的距离等于小圆的半径,
∴AB与小圆的位置关系是相切,
故答案为:相切.
