问题
填空题
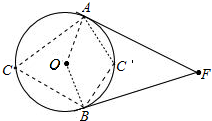
PA、PB切⊙O于A、B,∠APB=78°,点C是⊙O上异于A、B的任意一点,则∠ACB=______.
答案
如图,连接OA,OB,
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OB⊥PB,
∴∠AOB=180°-∠BPA=180°-78°=102°,
当C在优弧AB上,则∠ACB=
∠AOB=1 2
×102°=51°;1 2
当C在劣弧AB上,即C′点,则∠AC′B=180°-51°=129°.
故答案为:51°或129°.