问题
问答题
设二维正态随机变量(X，Y)的概率密度为f(x，y)．已知条件概率密度
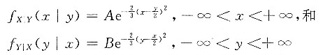
求(Ⅰ)常数A和B；
(Ⅱ)X和Y的边缘概率密度fX(x)和fY(y)；
(Ⅲ)f(x，y)和ρXY．
答案
参考答案：可由性质
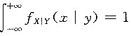，定出常数A．
也可以把
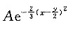看成形如
的正态分布N(μ，σ2)的概率密度
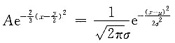所以
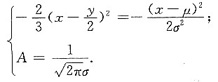
解得
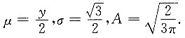
由对称性得
(Ⅱ)已知
所以
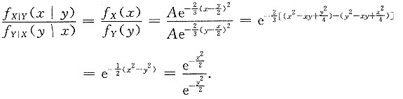
由于
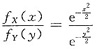，故可以得出
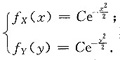其中C为常数．
显然
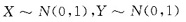
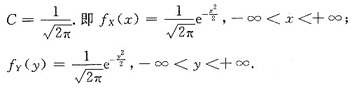
(Ⅲ)
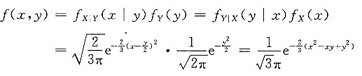
二维正态密度的一般形式为
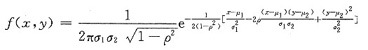
对此本题所求出的二维密度，可知μ1=μ2=0，σ1=σ2=1．
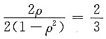；即2-2ρ2=3ρ，2ρ2+3ρ-2=0，
(2ρ-1)(ρ+2)=0，解得
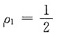，ρ2=-2(不可能)
所以
