参考答案：B

解析： 因函数f(x，y)具有连续的偏导数，从而函数f(x，y)可微，又因一元函数y=x²可导，故对复合函数f(x．x²)可用一阶全微分形式不变性求全微分，得
df(x，x²)=f’¹(x，x₂)dx+f’₂(x，x²)d(x²)
=f’₁(x，x²)dx+2xf’₂(x，x²)dx．
另一方面，由f(x，x²)=x⁴，又可得df(x，x²)=4x³出．于是
f’₁(x，x²)dx+2xf’₂(x，x²)dz

4x³dx．
在上式中令x=1，由题设及dx的任意性，即得
f’₁(1，1)+2f’₂(1，1)=4

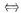f’_x(1，1)+2f’_y(1，1)=4

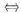f’_x(1，1)=4-2f’_y(1，1)=2．
[注意] 在本题的求解过程中f’₁(x，x²)，f’₂(x，x²)分别表示将二元函数f(x，y)对其第一个变量与对其第二个变量的偏导函数

，

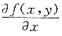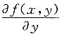中的第二个变量y换为x²后所得的复合函数，原因在于f(x，x²)其实是变量x的一元函数，从而记号f’_x(x，x²)的含义不清楚，不应当用它．